Missing the (Graphical) Forest for the (Statistical) Trees
Anscombe's Quartet and the Value of Visualization
"The Universe is full of dots. Connect the right ones and you can draw anything. The important question is not whether the dots you picked are really there, but why you chose to ignore all the others." - How Adam Smith Can Change Your Life
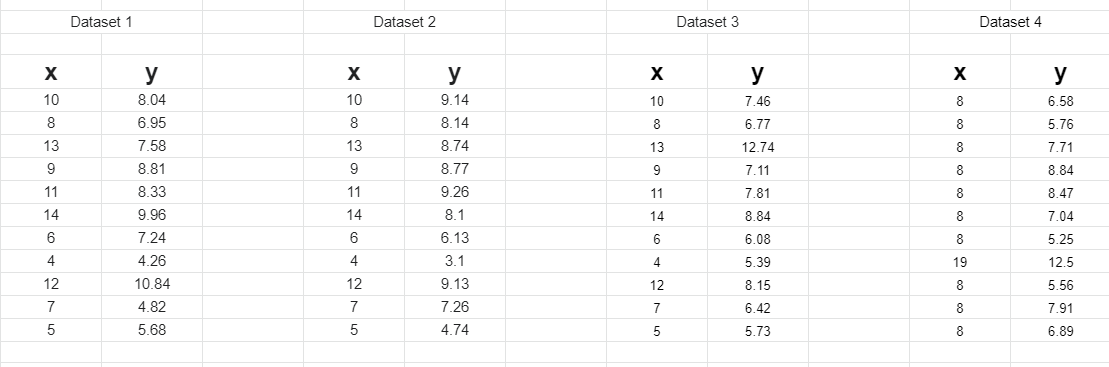
Above I have provided four datasets. Half of you are asleep already, I know. I’ll keep this brief.
If we want to understand the relationship between the independent variable (x) and the dependent variable (y) of these different datasets, what should we do? Let’s look at some simple summary statistics; the mean (average), the variance (how far from the average a number tends to be), and the correlation (a measure of how similar x and y are). We could also make a linear regression line (an equation of the classic format y = mx + b, that would allow you to plug in a new x, and predict the new corresponding y), you might also know of that as a “line of best fit”.
When you do that with these you’ll find for all four datasets individually:
Mean of x is 9.
Mean of y is 7.5.
Variance of x is 11.
Variance of y is 4.125.
Correlation between x and y is .816.
Line of best fit is y = .5x + 3
Given all these stats turn out to be identical for the different datasets, we would be excused for thinking that the relationships between their independent variables (x) and their dependent variables (y) would also be identical (or at least close).
Before we pat ourselves on the back for this insightful analysis of these datasets, let’s plot them on graphs so we have a visual representation of the relationships.
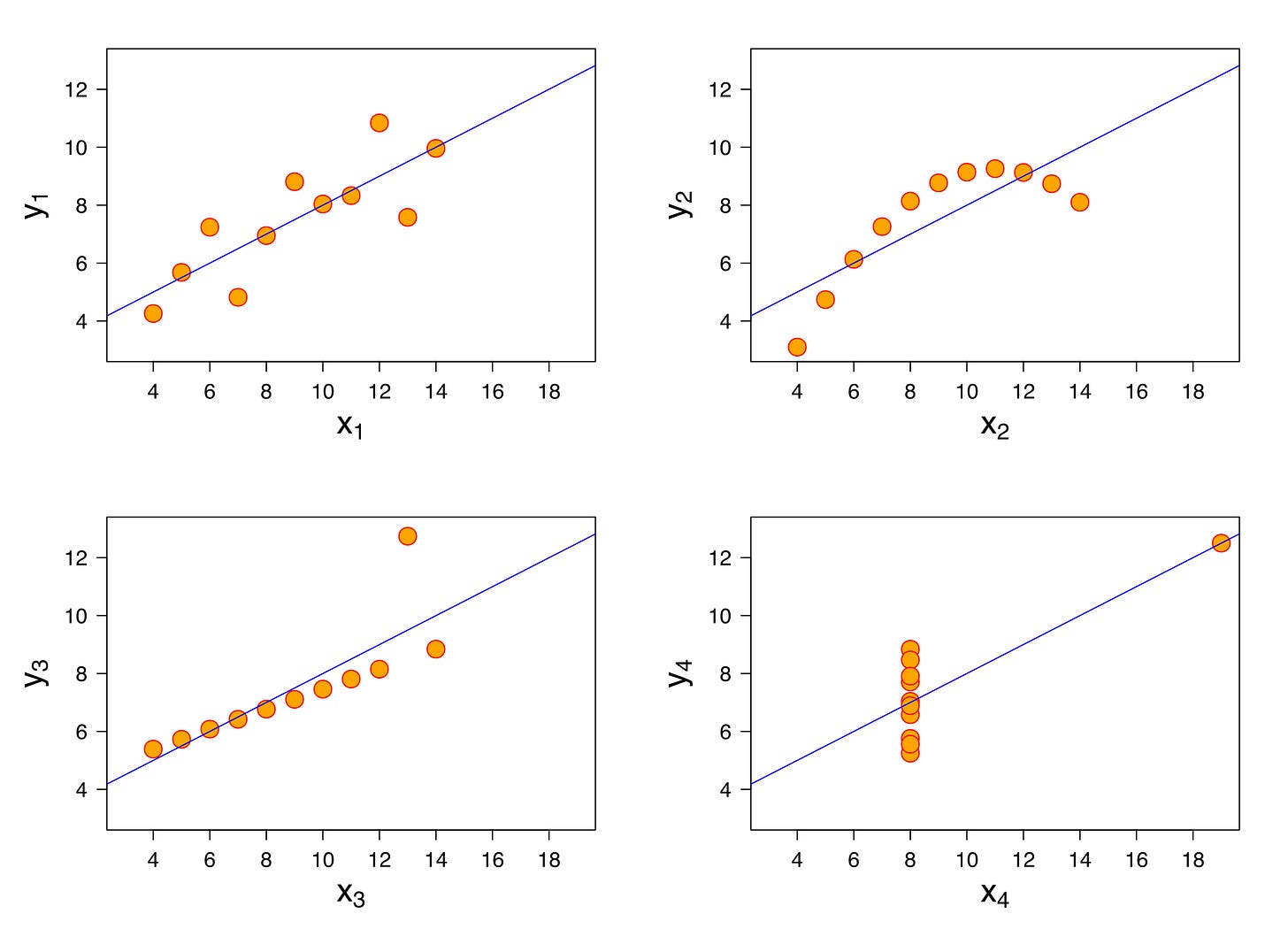
Uh oh. Clearly these four datasets are not describing similar things. Only in dataset 1 does it look like our line of best fit (shown in blue) is accurately describing the relationship between x and y. Dataset 3 looks vaguely similar; but given the smaller slope, if our x gets big or small enough we’re going to be way off on our prediction of y; and that’s before we even consider the huge outlier at x = 13. Datasets 2 and 4 look like they’re relationships that we would get fired if we told our boss were accurately described by the equation y = .5x + 3.
You can use your imagination to try and think of what kinds of real world phenomena these graphs could represent. The first one could be an NBA player’s points scored (y) in games as a function of shots taken in those games (x). The second one perhaps how delicious a snack is (y) as a function of how much salt it contains (x) .
These four datasets are called “Anscombe’s Quartet” and were created by the statistician Francis Anscombe to illustrate the importance of visualizing data in addition to analyzing it statistically. He described it as being a counter to the idea among statisticians that “numerical calculations are exact, but graphs are rough.”
Statistics don’t lie but they can easily be misinterpreted. Anscombe’s Quartet reminds us of one tool, visualization, that we can use to prevent us from drawing inaccurate conclusions from data.